Постквантовая криптография. Готовимся сегодня?

То, как могут повлиять на технологии криптографии и всей отрасли, базирующейся на их использовании, те новые возможности, которые могут открыться благодаря доступности квантовых вычислений, рассматривает Игорь Голдовский, директор Департамента инноваций, главный архитектор АО НСПК. Как и в своих предыдущих материалах, он выступает в качестве независимого эксперта в области платежных технологий, с чьим богатым опытом и всесторонней профессиональной экспертизой в области электронных платежей мы продолжаем знакомить наших читателей.

Предыдущие материалы: 1, 2.

Сегодня в СМИ, в том числе в профессиональных изданиях, периодически появляются материалы, посвященные вопросам создания и применения квантовых компьютеров. Все сходятся в том, что сегодняшние квантовые компьютеры, имеющие память в диапазоне от 50 до 100 кубитов, оказать заметного влияния на нашу повседневную жизнь не могут. Нужны машины, обладающие хотя бы несколькими тысячами кубитов памяти и работающие с невысокой вероятностью ошибки — не выше 0,5% на один кубит.

Никто не знает точного времени появления квантовых компьютеров с такими параметрами. Некоторые авторитетные эксперты утверждают, что это может случиться уже в 20-е годы нашего столетия. Другие специалисты говорят о том, что на достижение такого результата могут уйти десятилетия.

Не существует и ясного понимания спектра задач, которые могут успешно решаться с использованием квантовых компьютеров и непосильны для обычных компьютеров. На сегодняшний день можно уверенно говорить о следующих задачах, при решении которых преимущества квантовых компьютеров очевидны:

• задачи факторизации целых чисел и логарифмирования в конечном поле (о них будет сказано ниже), при решении которых квантовые компьютеры дают экспоненциальное ускорение в сравнении с классическими компьютерами. Решение этих задач лежит в основе практически всех применяемых алгоритмов асимметричного шифрования;
• задачи полного перебора: квантовый компьютер позволяет получить здесь квадратичное ускорение, что, например, потребует увеличения размера ключей в симметричных алгоритмах шифрования;
• задачи моделирования физических и химических систем. Грубо говоря, квантовый вероятностный характер вычислений позволяет параллельно моделировать различные состояния подобных систем.

Цель настоящей статьи — проанализировать угрозы для используемых сегодня криптографических схем от ожидаемого в недалеком будущем появления квантовых компьютеров производительностью в несколько тысяч кубитов, а также рассказать о новых перспективных криптографических методах для минимизации влияния квантовых технологий на криптостойкость средств защиты информации.

Что можно и что нельзя взломать с помощью квантовых вычислений?

Как будет рассказано ниже, для квантовых компьютеров были придуманы алгоритмы (алгоритмы Шора и Гровера (Shor Grover)), оказывающие существенное влияние на криптостойкость сегодняшних криптографических алгоритмов [Circuit for Shor’s algorithm using 2n+3 qubits. Stephane Beauregard, 2003; Shor’s discrete logarithm quantum algorithm for elliptic curves. John Proos, Christof Zalka, 2008]. В частности, наиболее широко используемые на практике алгоритмы асимметричного шифрования RSA, DSA, ECDSA, EdDSA, EC-SDSA перестают быть криптостойкими и взламываются (находится секретный ключ) за полиномиальное от размера публичного ключа время. Это утверждение верно для любых алгоритмов асимметричного шифрования, криптостойкость которых базируется на трудоемкости решения математических задач факторизации (разложения числа на простые сомножители) и дискретного логарифмирования в конечном поле или на множестве точек эллиптической кривой. Другими словами, все массово используемые алгоритмы асимметричного шифрования требуется менять на алгоритмы, криптостойкость которых базируется на трудоемкости решения неких иных математических задач!

Последствия от появления квантовых компьютеров для алгоритмов симметричного шифрования и хэш-функций не столь катастрофичны. Например, ниже будет показано, что криптостойкость любого симметричного алгоритма шифрования при использовании квантового компьютера эквивалентна криптостойкости того же алгоритма при использовании классического компьютера, но с увеличенной в два раза длиной ключа шифрования. Другими словами, в случае симметричных алгоритмов шифрования можно просто удвоить длину ключа, чтобы добиться прежней криптостойкости, не меняя при этом криптографического алгоритма.

Конечно, увеличение длины ключа приведет к увеличению времени шифрования. Но это естественное развитие событий: растет производительность компьютеров и их количество, а значит, растут вычислительные ресурсы для проведения атак. Чтобы от них защититься, нужно увеличивать размер симметричного ключа. Факт грядущего появления квантовых компьютеров лишь скачкообразно ускоряет этот процесс.

В то же время существуют алгоритмы шифрования, которые «ломаются» с помощью квантовых алгоритмов за полиномиальное время. В качестве примера можно привести варианты алгоритма DES: 2K-DES (выполняет 64 раунда шифрования 96 битным ключом, который представляется в виде двух 48 битных половинок, поочередно используемых в раундах алгоритма) и 4K-DES (то же количество раундов выполняется с уже 192 битным ключом, который представляется в виде четырех поочередно используемых 48 битных частей). С помощью квантового алгоритма Саймона (Simon) ключи этих алгоритмов находятся за полиномиальное время.

Следует отметить, что эти алгоритмы относительно просто вскрываются и с помощью классических компьютеров с использованием так называемой сдвиговой атаки, изобретенной Алексом Бирюковым (Alex Biryukov) и Дэвидом Вагнером (David Wagner). Для вскрытия 2K-DES с помощью этой атаки требуется всего 2³² известных открытых текстов и 2³³ операций шифрования. Однако тот же алгоритм Саймона позволяет вскрыть российский алгоритм шифрования, определенный в стандарте ГОСТ Р28147–89, используя 2^114.8 квантовых запросов, что в 2^13.2 раз быстрее, чем вскрытие этого алгоритма шифрования с помощью алгоритма Гровера (квантового перебора ключей).

Еще меньшее влияние появление квантовых компьютеров окажет на стойкость хэш-функций (под стойкостью в данном случае понимается трудоемкость решения задачи поиска коллизии хэш-функции). Асимптотически потребуется увеличить длину значения хэш-функции в полтора раза. Например, вместо функции SHA-256 потребуется применять функцию SHA-384.

Что делать?

Как мы видим, последствия от появления квантовых компьютеров значительные, а поскольку криптография сегодня используется массово (достаточно в качестве примера привести протокол TLS, практически постоянно используемый пользователями интернета), то готовиться к их появлению нужно уже сегодня. Именно так рассудил Национальный институт по стандартизации США (NIST), который еще в 2016 году запустил проект PQC (Post-Quantum Cryptography) Standardization.

У проекта PQC (Post-Quantum Cryptography) Standardization три задачи:

1. Заменить схемы создания цифровой подписи, определенные в стандарте FIPS 186–4 (RSA, DSA, ECDSA)
2. Заменить протокол шифрования данных при передаче ключей, определенный в SP 800–56B и основанный на использовании RSA
3. Заменить протокол согласования ключей, определенный в SP 800–56A, в основе которого лежит алгоритм Диффи- Хеллмана (Diffie- Hellman).

В конце 2016 года NIST выпустил сообщение (Federal Notice) о сборе предложений по решению перечисленных задач до конца 2017 г. В 2018 г. NIST приступил к анализу полученных многочисленных предложений и планирует до конца 2023 г. завершить выбор алгоритмов, решающих поставленные задачи. При этом допускается выбор нескольких победителей. Из сообщения NIST: We may not be able to select one single winner for each function (signature, encryption, key agreement).

NIST также внимательно изучает процесс миграции со старых алгоритмов на новые. Речь идет о работе в т. н. гибридной моде, когда какие-то пользователи пока поддерживают только старые алгоритмы. Предполагается, что наряду с поддержкой новых алгоритмов пользователи должны будут в течение какого-то времени поддерживать и старые алгоритмы. Такие продвинутые пользователи будут генерировать подпись документа с использованием старого и нового алгоритмов, и продвинутым пользователем подпись будет признаваться при наличии двух подписей сообщения и только когда обе подписи верны.

NIST предполагает, что миграция на постквантовые криптографические алгоритмы начнется в 2030 году. До этого времени ожидается использование в основном сегодняшних стандартов FIPS.

Состояние дел с построением квантовых компьютеров

Как следует из сказанного выше, виновником будущего переполоха в криптографии могут стать квантовые компьютеры. Причем не просто квантовые компьютеры, а, как будет показано ниже, компьютеры, способные поддержать несколько тысяч надежно функционирующих кубитов. Каково же положение дел с построением таких компьютеров в наши дни?

Сегодняшними мировыми лидерами в построении универсальных квантовых компьютеров являются компании Google, IBM и Intel. В марте 2018 года компания Google объявила, что ей удалось построить 72 кубитный квантовый процессор Bristlecone, имеющий низкую вероятность ошибок в вычислениях: вероятность ошибки в 2 кубитном логическом элементе процессора Bristlecone составляет 0,6%, что чуть выше уже упоминавшегося нами значения (0,5%), установленного в техническом задании на разработку. Компания не раскрыла подробных характеристик своего устройства, однако утверждает, что оно позволяет достичь «квантового превосходства».

Чуть раньше, в ноябре 2017 года, компания IBM сообщила о создании и успешном испытании процессора с 50 кубитами, а в январе 2018 г. исполнительный директор компании Intel Брайан Кржанич (Brian Krzanich) сообщил о создании сверхпроводящего квантового чипа под кодовым названием «Tangle Lake», обладающего 49 кубитами.

Несколько отдельно от лидеров стоит канадская компания D-Wave Systems со своими адиабатическими компьютерами, которая заявляет о создании различных вариантов квантового компьютера: от 16 кубитного до 2000 кубитного. Компьютеры D-Wave пригодны для решения лишь узкого класса задач (например, задачи поиска глобального минимума функции). Некоторые исследователи высказывали сомнения в том, что в компьютерах компании действительно достигается существенное «квантовое ускорение». В декабре 2015 г. специалисты компании Google подтвердили, что, согласно их исследованию, компьютер D-Wave использует квантовые эффекты. При этом в «1000 кубитном» компьютере кубиты в действительности организованы в кластеры по 8 кубитов каждый. Тем не менее это позволило добиться быстродействия в 100 млн раз больше (по сравнению с обычным компьютером) в одном из алгоритмов (алгоритме поиска глобального минимума функции).

Компьютеры D-Wave предлагаются на рынке по ценам 10–15 млн долл. США и уже приобретались компаниями Google, Lockheed Martin, Temporal Defense Systems, а также агентством NASA и Лос- Аламосской национальной лабораторией.

Как следует из короткого обзора по состоянию дел с разработкой универсальных квантовых компьютеров, их сегодняшние возможности на два порядка ниже того, что требуется для взлома криптографических алгоритмов. Построить квантовый компьютер, поддерживающий большое количество кубитов, совсем непросто, поскольку роль кубитов выполняется сверхминиатюрными хрупкими по своей природе квантовыми системами размера электрона или фотона, которые требуется поддерживать в стабильном состоянии в течение достаточно долгого времени (хотя бы в течение нескольких секунд). Кроме того, такие квантовые системы подвержены многочисленным внешним воздействиям (в первую очередь электромагнитным воздействиям), которые приводят к появлению ошибок вычислений. Теоретически такие ошибки, если их не очень много, можно исправлять, используя дополнительные кубиты, предназначенные для исправления ошибок с помощью специальных помехоустойчивых квантовых кодов. На практике же получается, что для обеспечения надежных квантовых вычислений количество таких дополнительных кубитов, предназначенных для исправления ошибок, сравнимо с количеством полезных кубитов, применяемых для квантовых вычислений.

В настоящее время для создания кубитов и, следовательно, построения квантовых компьютеров применяются всего два подхода (раньше их было существенно больше: от использования ядерного магнитного резонанса и поляризованных фотонов до применения квантовых точек — электронов, захваченных группой атомов): это ионные ловушки и сверхпроводящие нанокольца. Ионные ловушки представляют собой одномерный кристалл, состоящий из ионов, находящихся в электромагнитном поле. Ионы в кристалле взаимодействуют друг с другом, обмениваясь колебательными возбуждениями. Изменение состояния кубита в соответствии с заданным алгоритмом происходит за счет воздействия поляризованного лазерного пучка на один или группу ионов.

Сверхпроводящие нанокольца, расположенные в магнитном поле при температуре, близкой к абсолютному нулю, поддерживают ток, текущий в кольце в противоположных направлениях. Тем самым моделируется кубит, способный одновременно находиться в двух состояниях.

Как уже отмечалось, точное время появления квантовых компьютеров, реально представляющих угрозу современной криптографии, сегодня спрогнозировать невозможно — на это может потребоваться от нескольких лет до десятилетий. История показывает, что на начальном этапе развития новой технологии часто возникают прорывные идеи, значительно сокращающие сроки ее внедрения.

Алгоритм Шора

В 1995 году исследователь компании AT&T Питер Шор (Peter Shor) опубликовал статью Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer («Алгоритм полиномиальной сложности для разложения числа на простые множители и дискретного логарифмирования на квантовом компьютере»). Алгоритм Шора является квантовым алгоритмом (предназначен для исполнения на квантовом компьютере) и позволяет добиться экспоненциального ускорения при решении математических задач факторизации, дискретного логарифмирования в конечном поле (DLP) и дискретного логарифмирования на множестве точек эллиптической кривой (ECDLP). Эти задачи при определенных практически важных значениях параметров невозможно за обозримое время решить на классическом компьютере, но их решение возможно на квантовом компьютере. Это, в свою очередь, означает, что с появлением квантового компьютера будет возможно взломать такие широко используемые на практике алгоритмы асимметричного шифрования, как RSA, Diffie–Hellman, DSA, ECDSA, EC-SDSA, EdDSA, криптостойкость которых базируется на сложности решения перечисленных выше математических задач. Другими словами, статью Шора можно было бы назвать Breaking All Public- Key Crypto on a Quantum Computer («Компрометация всей асимметричной криптографии на квантовом компьютере»). Алгоритм Шора был назван известным специалистом в теории сложности Скотом Ааронсоном (Scott Joel Aaronson) одним из главных научных достижений конца ХХ века.

Отметим, что лучший классический алгоритм факторизации числа N требует времени, экспоненциально зависящего от n, где n = log N. В то же время алгоритм Шора на квантовом компьютере требует полиномиального времени от n, а именно O(n²log₂n(log₂log₂n)) операций. На практике это означает экспоненциальное ускорение решения проблемы факторизации: на квантовом компьютере для компрометации схемы RSA вместо тысяч лет потребуется несколько часов, дней, недель, месяцев.

В работе [1] показано, что для факторизации числа длиной n бит достаточно иметь квантовый компьютер, использующий 2n+3 кубитов, содержащий O(n³log₂n) элементарных гейтов глубиной O(n³). Для взлома алгоритма RSA с модулем открытого ключа 2048 битов требуется квантовый компьютер, содержащий 4099 кубитов.

Проблема дискретного логарифмирования DLP состоит в следующем: по произвольным заданным значениям y, g и простого p требуется найти значение x такое, что y = gx (mod p). Решение задачи DLP на классическом компьютере требует экспоненциально большого от p количества времени (операций), в то время как алгоритм Шора поиска периода функции позволяет решить задачу за полиномиальное время.

И снова сложность задачи нахождения значения x равна O(n²log₂n(log₂log₂n)) , где n –длина в битах числа p. Следовательно, решение проблемы DLP на квантовом компьютере при использовании алгоритма Шора имеет полиномиальную сложность.

Аналогичным образом полиномиальная сложность задачи дискретного логарифмирования ECDLP (Elliptic Curve Discrete Logarithm Problem) на точках эллиптической кривой. Задача требует решения уравнения Y = xP относительно х при заданных точках кривой P и Y.

В работе [2] показано, что для решения проблемы ECDLP для кривой n битов существует алгоритм с разделением регистров, требующий поддержки

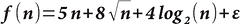
кубитов, где ε — константа, приблизительно равная 10. Отсюда для наиболее актуальных значений n получаем f(256) = 1500 кубитов, f(512) = 2800 кубитов.

Алгоритм Гровера

Вслед за алгоритмом Шора, обеспечивающим экспоненциальное ускорение решения задач факторизации и логарифмирования, для квантовых компьютеров был придуман алгоритм Гровера, который обеспечивает квадратичное ускорение решения задачи поиска по неструктурированной БД. Этот алгоритм был впервые опубликован в 1996 году. Предположим, что некоторая величина x принимает n различных значений. Пусть на m значениях х функция f(x) принимает значение 1, а на остальных (n-m) значениях х выполняется равенство f(x) = 0. Задача состоит в поиске любого значения x, при котором f(x) = 1. Можно показать, что на обычном классическом компьютере для решения задачи потребуется

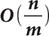
операций. В то же время при использовании алгоритма Гровера на квантовом компьютере для решения задачи потребуется

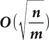
операций, т. е. наблюдается квадратичное ускорение решения задачи, хотя и не такое значительное, как при использовании алгоритма Шора для решения задачи факторизации на квантовом компьютере.

Посмотрим, какие последствия на стойкость криптографических алгоритмов оказывает алгоритм Гровера. Рассмотрим функцию f(x), которая принимает значение 1 тогда и только тогда, когда x равно неизвестному значению секретного ключа K, при котором выполняется равенство E(K, P) = C для некоторых известных значений шифруемого текста P и соответствующего ему шифротекста C и некоторой известной функции шифрования E(). На практике это означает, что для поиска 128 битного ключа AES на квантовом компьютере требуется время, пропорциональное 2⁶⁴, а не 2¹²⁸, как на классическом компьютере. Потребуется также достаточно большое количество шифруемых текстов, чтобы гарантировать уникальность ключа. Трудоемкость 2⁶⁴ операций существенно меньше 2¹²⁸, что означает, что найти ключ на квантовом компьютере значительно проще, чем на классическом.

Однако существует простое решение для восстановления криптостойкости алгоритма AES при использовании квантового компьютера. Чтобы обеспечить криптостойкость, получаемую на классическом компьютере при применении 128 битового ключа, на квантовом компьютере нужно использовать 256 битный ключ! Алгоритм Гровера уменьшит сложность решения задачи поиска ключа «всего» до

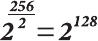
операций шифрования.

Алгоритм Гровера также позволяет более эффективным образом искать прообразы значений хэш-функции Hash(). Определим задачу поиска прообраза значения h хэш-функции Hash() через следующую функцию f(): «f(x) = 1 тогда и только тогда, когда Hash(x) = h, в противном случае f(x) = 0». Алгоритм Гровера на квантовом компьютере позволит найти прообраз значения h n-битовой хэш-функции за

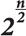
операций. Как и в случае с шифрованием, чтобы обеспечить безопасность 2ⁿ на квантовом компьютере, нужно использовать хэш-функции с удвоенной длиной их значений. Для поиска прообраза хэш-функции размером 2n бит на квантовом компьютере с помощью алгоритма Гровера потребуется порядка 2ⁿ операций вычисления значения хэша.

Отметим, что квантовые вычисления позволяют также находить коллизии хэш-функции за время, пропорциональное

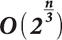
, вместо

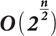
при использовании классической атаки birthday attack. Отсюда можно заключить, что квантовые компьютеры могут превосходить классические и при решении задачи поиска коллизий для хэш-функций. Однако алгоритм поиска коллизий, требующий времени, пропорционального

, также требует для своей работы памяти, пропорциональной

.

Можно показать, что при использовании такого объема памяти на классическом компьютере можно распараллелить вычисления, и поиск коллизии в этом случае займет время, пропорциональное

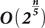
, что значительно меньше времени

, требуемого для решения задачи на квантовом компьютере.

Из сказанного выше следует вывод: применение квантового компьютера делает полностью бесполезным все сегодня массово используемые алгоритмы асимметричного шифрования, основанные на сложности решения задачи факторизации, DLP и ECDLP.

В то же время существует простая возможность обеспечить требуемую криптостойкость симметричных алгоритмов шифрования, просто удваивая размер используемых в них ключей.

Постквантовая криптография

В качестве ответа на вызовы квантовых вычислений была разработана целая серия новых криптографических алгоритмов, не подверженных атакам с использованием квантовых вычислений. Ниже приведены некоторые из них:

• система Мак-Элиса (code-based algorithm). Используется двоичный код Гоппы, исправляющий большое число ошибок и для которого существует эффективный алгоритм декодирования. Если код выбирается из достаточно большого класса кодов, то угадать, какой именно код был выбран, практически невозможно. Порождающая матрица кода Гоппы преобразуется до такой степени, что получившаяся в результате матрица выглядит случайной. Таким образом, криптоаналитик должен решить общую задачу декодирования линейных кодов, т. е. задачу поиска ближайшего кодового слова к произвольному слову, которая является NP-полной задачей;
• алгоритмы на решетках (lattice-based algorithms). Базируются на решении следующих NP-трудных задач: 1) определения короткого базиса по длинному базису (Short Basis Problem) решетки (специальной математической структуры) или 2) поиска точки решетки, заданной длинным базисом, ближайшей к произвольной точке n-мерного пространства (Closest Vector Problem, или CVP). Наиболее популярны в криптографии на решетках вариации задачи CVP;
• алгоритмы на базе систем квадратичных уравнений (multivariate algorithm). Задача нахождения решения квадратичной системы линейных уравнений со многими неизвестными (multivariate quadratics, или MQ) является NP-трудной, и это является основой для построения криптографических алгоритмов;
• алгоритмы на основе хэш-функций (hash-based algorithm). В отличие от остальных рассмотренных здесь схем постквантовой криптографии криптография на основе хэш-функций базируется на безопасности криптографических хэш-функций (трудоемкости задачи поиска прообраза), а не на решении трудных математических проблем типа факторизации и логарифмирования в конечном поле. Как было показано ранее, квантовый компьютер обеспечивает всего лишь квадратичное ускорение в решении задачи нахождения прообраза для хэш-функции, а потому криптографические алгоритмы на основе хэш-функций могут с успехом использоваться и в постквантовой криптографии. Сами по себе криптографические алгоритмы на основе хэш-функций достаточно сложные. Примером алгоритма этого класса является алгоритм формирования одноразовой подписи, предложенный Винтерницем (Winternitz) в 1979 году (WOTS, или Winternitz One-Time Signature).
• Протокол Диффи-Хеллмана с использованием суперсингулярной изогении (Supersingular isogeny Diffie-Hellman key exchange, SIDH). Основан на сложности решения следующей задачи. Даны две изогенные эллиптические кривые E₁ и E₂ с различными j–инвариантами (известная характеристика эллиптической кривой). Требуется найти изогению (специальное рациональное преобразование) между кривыми E₁ и E₂.

С подробным описанием алгоритмов постквантовой криптографии можно ознакомиться во 2 и 3 номерах журнала «Платежные Технологии».

Фото: предоставлено автором